问答题

什么是数据结构？有关数据结构的讨论涉及哪3个方面？

答：按某种逻辑关系组织起来的一组数据元素，按一定的存储方式存储于计算机中，并在其上定义了一个运算的集合，称为一个数据结构。
数据结构涉及以下三方面的内容：
（1）数据成员以及它们相互之间的逻辑关系，也称为数据的逻辑结构。
（2）数据元素及其关系在计算机存储器内的存储表示，也称为数据的物理结构，简称为存储结构。
（3）施加于该数据结构上的操作，即运算。

什么是算法？算法的5个特性是什么？

答：通常算法定义为解决某一特定任务而规定的一个指令序列。一个算法应当具有以下特性。
（1）有穷性：一个算法无论在什么情况下都应在执行有穷步后
结束。（2）确定性：算法的每一步都应确切地、无歧义地定义。对于每一种情况，需要执行的动作都应严格地、清晰地规定。
（3）可行性：算法中每一条运算都必须是足够基本的。也就是
说，它们原则上都能精确地执行，甚至人们仅用笔和纸做有限
次运算就能完成。（4）输入：一个算法必须有0个或多个输入。它们是在算法开始运算前给予算法的量。这些输入取自特定的
对象的集合。它们可以使用输入语句由外部提供，也可以使用
赋值语句在算法内给定。（5）输出：一个算法应有一个或多个
输出，输出的量是算法运算的结果。

简述顺序表和链表存储方式的主要优缺点。

答：顺序表的优点是可以随机存取元素，存储密度高，结构简单；缺点是需要一片地址连续的存储空间，不便于插入和删除元素（需要移动大量的元素），表的初始容量难以确定。链表的优点是便于结点的插入和删除（只需要修改指针属性，不需要移动结点），表的容量扩充十分方便：缺点是不能进行随机访问，只能顺序访问，另外每个结点上增加指针属性，导致存储密度较低。

带头结点的双链表和循环双链表相比有什么不同？在何时使用循环双链表？

答：在带头结点的双链表中，尾结点的后继指针为None，头结点的前驱指针不使用；在带头结点的循环双链表中，尾结点的后继指针指向头结点，头结点的前驱指针指向尾结点，当需要快速找到尾结点时，可以使用循环双链表。

什么叫“假溢出”？如何解决假溢出？

答：在非循环顺序队中，当队尾指针已经到了数组的上界，不能再做进队操作，但其实数组中还有空位置，这就叫“假溢出”。解决假溢出的方式之一是采用循环队列。

如果某个一维整数数组A的元素个数n很大，存在大量的重复元素，且所有值相同的元素紧跟在一起，请设计一种压缩存储方式使得存储空间更节省。

答：采用元素类型形如“[整数，个数]”的列表压缩存储，例如数组A为{1,1,1,5,5,5,5,3,3,3,3,4,4,4,4,4,4},共有17个元素，对应的压缩存储为[[1,3],[5,4],[3,4],[4,6]],在压缩列表中只有8个整数，从中看出，重复元素越多，采用这种压缩存储方式越节省存储空间。

已知一颗完全二叉树的第6层（设根结点为第1层）有8个叶子结点，则该完全二叉树的结点个数最多是多少？最少是多少？

答：完全二叉树的叶子结点只能在最下面两层，对于本题而言，结
点最多的情况是第6层为倒数第二层，即16层构成一棵满二叉树，
其结点总数为26-1=63。其中第6层有25=32个结点，含8个叶子结点，则另外有32-8=24个非叶子结点，它们中每个结点都有两个孩子结点（均为第7层的叶子结点），计为48个叶子结点。这样最多的结点个数＝63+48=111。
结点最少的情况是第6层为最下层，即15层构成一棵满二叉树，其结点总数为25-31=31，再加上第6层的结点，总计31+8=39。这样最少的结点个数为39。

已知一颗完全二叉树有50个叶子结点，则该二叉树的总结点数至少应有多少个？

答：n0=50,n=n0+n1+n2,度之和=n-1=n1+2*n2,由此推出n2=49,这样
n=n1+99，所以当n1=0时n最少，因此n至少有99个结点。

若干个包含不同权值的字母已经对应好一组哈夫曼编码，如果某个字母对应的编码为001，则什么编码不可能对应其他字母？什么编码肯定对应其他字母？

由哈夫曼树的性质可知，以0、00和001开头的编码不可能对应
其他字母。该哈夫曼树的高度至少是3,其最少叶子结点的情况如图1. 6所示，因此以000、01和1开头的编码肯定对应其他字母。

采用普里姆（Prim）算法从顶点1出发构造出下图1.8的一颗最小生成树。

答：采用普里姆（Prim）算法构造最小生成树的过程如图1.13所示。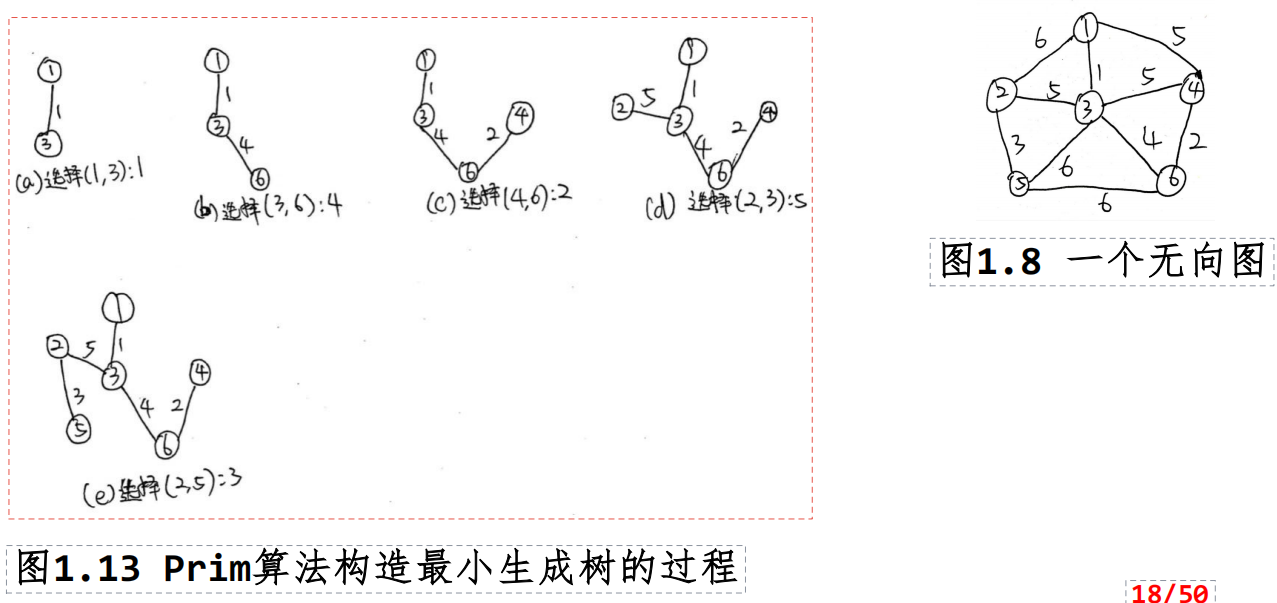

采用克鲁斯卡尔（Kruskal）算法构造出下图1.8的最小生成树。

答：采用克鲁斯卡尔（Kruskal）算法构造最小生成树的过程如图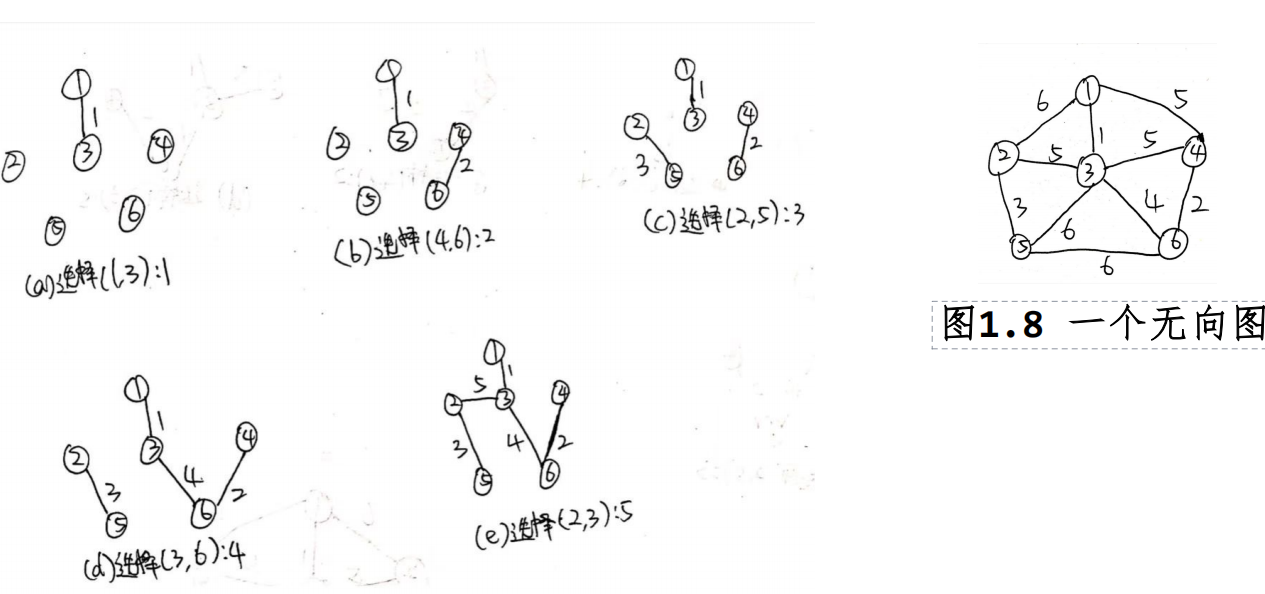

1.13所示。

设图中顶点表示村庄，有向边代表交通路线，若要建立一家医院，试问建在哪个村庄能使各村庄的总体交通代价最小。

答：采用Floyd算法求出两顶点之间的最短路径长度。其邻接矩阵如下：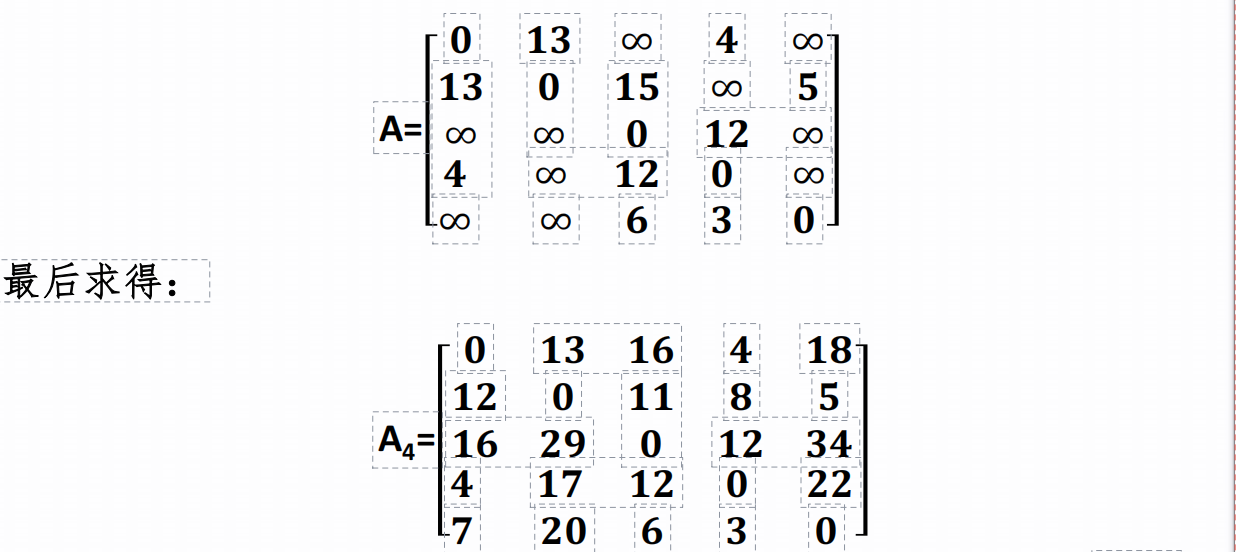

答:(接上页)
从A4中求得每对村庄之间的最少交通代价。假设医院建在i村庄时其他各村庄往返总的交通代价如表1.2所示，显然把医院建在村庄3时总体交通代价最少。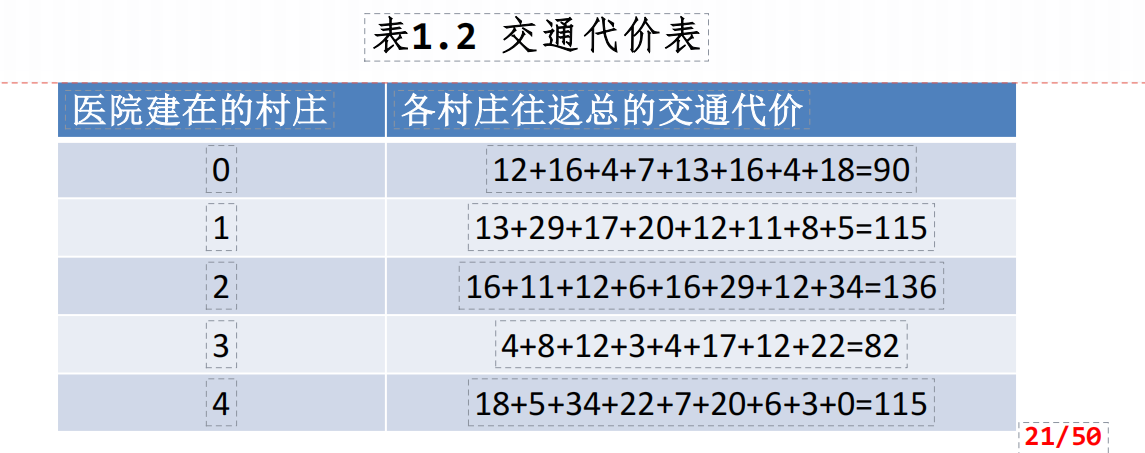

假设一颗二叉排序树的关键字为单个字母，其后序遍历序列为ACDBFIJHCGE，回答以下问题。（1）画出该二叉排序树。（2）求在等概率下的查找成功的平均查找长度。（3）求在等概率下的查找不成功的平均查找长度。

答：（1)该二叉排序树的后序遍历序列为ACDBFIJHGE,则中序遍历
序列为ABCDEFGHIJ,由后序序列和中序序列构造的二叉排序树如图1.
23所示。
(2)ASL成功＝（1x1+2x2+4x3+2x4+1x5)/10=3。
(3)ASL不成功＝（6x3+3x4+2x5)/11=3.64。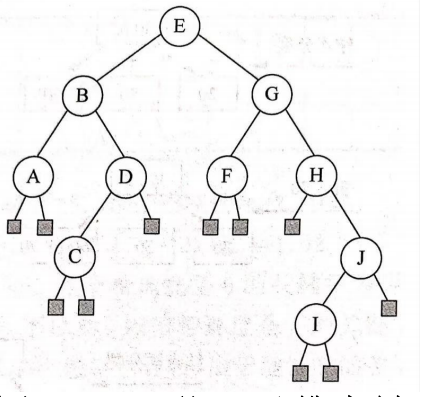

设有一组关键字为（19，1，23，14，55，20，84，27，68，11，10，77），其哈希函数为h（key）=key%13，采用开放地址法的线性探测法解决冲突，试在0～18的哈希表中对该关键字序列构造哈希表，并求在成功情况下的平均查找长度。

答：依题意，n=12,m=19。利用线性探测法计算下一地址的计算公 式为：
d0=h(key)
dj+1=(dj+1)%m j=0,1,…
计算各关键字存储地址的过程如下：
h(19)=19%13=6
h(1)=1%13=1
h(23)=23%13=10
h(14)=14%13=1 冲突
d0=1,d1=(1+1)%19=2
h(55)=55%13=3
h(20)=20%13=7
h(84)=84%13=6 冲突
d0=6,d1=(6+1)%19=7 仍冲突
d2=(7+1)%19=8
h(27)=27%13=1 冲突
d0=1,d1=(1+1)%19=2 仍冲突
d2=(2+1)%19=3 仍冲突
d3=(3+1)%19=4
h(68)=68%13=3 冲突
d0=3,d1=(3+1)%19=4 仍冲突
d2=(4+1)%19=5
h(11)=11%13=11
h(10)=10%13=10 冲突
d0=10,d1=(10+1)%19=11 仍冲突
d2=(11+1)%19=12
h(77)=77%13=12 冲突
d0=12,d1=(12+1)%19=13
因此，构建的哈希表如表1.3所示。

表1.3中的探测次数即为相应关键字成功查找时所需比较关键字的次 数，因此：
ASL成功=（1+2+1+4+3+1+1+3+1+1+3+2）/12=1.92

请回答下列关于堆排序中堆的两个问题：（1）堆的存储表示是顺序的还是链式的？（2）设有一个小根堆，即堆中任意结点的关键字均小于它的左孩子和右孩子的关键字，其中具有最大关键字的结点可能在什么地方？

答：（1)通常，堆的存储表示是顺序的。因为堆排序将待排序序列
看成是一棵完全二叉树，然后将其调整成一个堆，而完全二叉树特
别适合于采用顺序存储结构，所以堆的存储表示采用顺序方式最合
适。
（2)小根堆中具有最大关键字的结点只可能出现在叶子结点中，因
为最小堆的最小关键字的结点必是根结点，而最大关键字的结点由
偏序关系可知，只有叶子结点可能是最大关键字的结点。

程序题

有两个集合采用整数顺序表A、B存储，设计一个算法求两个集合的差值C，C仍然用顺序表存储，并给出算法的时间和空间复杂度。例如A=（1，3，2），B=（5，1，4，2），并集C=（3）。
解：将集合A中所有不属于集合B的元素添加到C中，最后返回C。对应的算法如下：

1
2
3
4
5
6
def Diff(A,B):
    C=SqList()
    for iinrange(0,A.getsize()):  #将A中不属于B的元素添加到C中
        if B.GetNo(A[i]==-1):
            C.Add(A[i])
        return C

有一个递增有序的整数双链表L，其中至少有两个结点，设计一个算法就地删除L中所有值重复的结点，即多个相同值重复的结点仅保
留一个。例如，L=（1，2，2，2，3，5，5），删除后L=（1，2，3，
5）。
解：在递增有序的整数双链表L中，值相同的结点一定是相邻的。首先
让pre指向首结点，p指向其后续结点，然后循环，直到p为空为止：
（1）若p结点值等于前驱结点（pre结点）值，通过pre结点删除p结点，置p=pre.next。
(2)否则，pre、p同步后移一个结点。
对应的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
def Delsame(L):
    pre=L.dhead.next 
    p=pre.next
    while p!=None:
        if p.data==pre.data:
            pre.next=p.next
            if p.next!=None:
                p.next.prior=pre
            p=pre.next
        else:
            pre=p
            p=pre.next

给定一个字符串str,设计一个算法采用顺序栈判断str是否为形如“序列1@序列2”的合法字符串，其中序列2是序列1的逆序，在str中恰好只有一个@字符。
解：设计一个栈st，遍历str，将其中‘@’字符前面的所有字符进栈，再扫描str中‘@’字符后面的所有字符，对于每个字符ch，退栈一个字符，如果两者不相同，返回False。当循环结束时，若str扫描完毕并且栈空，返回True,否则返回False。对应的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def match(str)：
    st=SqStack()   #定义一个顺序栈
    i=0
    while i<len(str) and str[i]!=‘@’:
        st.push(str[i])i+=1
    if i==len(str): 
        return False
    i+=1
    while i<len(str) and not st.empty():  #str没有扫描完毕并且栈不空，循环
        if str[i]!=st.pop():     #两者不等返回False
            return False
        i+=1
        if i<len(str) and st.empty():  #str扫描完毕并且栈空返回True
        return True 
        else:
            return False

有一个整数数组a，设计一个算法将所有偶数位元素移动到所有奇数位元素的前面，要求它们的相对次序不改变。例如，
a={1,2,3,4,5,6,7,8},移动后a={2,4,6,8,1,3,5,7}。
解：采用两个队列来实现，先将a中的所有奇数位元素进qu1队中，所有偶数位元素进qu2队中，再将qu2中的元素依次出队并放在a中，qu1中的元素依次出队并放到a中。对应的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
defMove():
    qu1=CSqQueue()   #存放奇数位元素
    qu2=CSqQueue()    #存放偶数位元素
    i=0
    while i<len(a):
        qu1.push(a[i])     #奇数位元素进qu1队
        i+=1
        if i<len(a):
            qu2.push(a[i])     #偶数位元素进qu2队
            i+=1
        i=0
        while not qu2.empty():    #先取qu2队列的元素
            a[i]=qu2.pop()
            i+=1
        while not qu1.empty():    #再取qu1队列的元素
            a[i]=qu1.pop()
            i+=1

假设字符串s采用String对象存储，设计一个算法，在串s
中查找子串t最后一次出现的位置。例如，s=“abcdabcd”,
t=“abc”,结果为4.
（1）采用BF算法求解。
（2）采用KMP算法求解。
解：用lasti记录串s中子串t最后一次出现的位置（初始为-1），修改BF算法和KMP算法，在s中找到一个t后用lasti记录其位置，此时
i指向s中t子串的下一个字符，将j置为0继续查找。对应的算法如下：MaxSize=100
#基于BF算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def BF(s,t): 
    lasti=-1
    i,j=0,0
    while i<s.getsize() and j<t.getsize():
        if s[i]==t[j]:
            i,j=i+1,j+1
        else:
            i,j=i-j+1,0
        if j>=t.getsize(): 
            lasti=i-t.getsize()
            i=i-j+1
            j=0
        return lasti
def GetNext(t,next):
    j,k=0,-1
    next[0]=-1
    while j<t.getsize()-1:
        if k==-1 or t[j]==t[k]:  #j遍历后缀，k遍历前缀
            j,k=j+1,k+1 
            next[j]=k
        else:
            k=next[k]
def KMP(s,t):  
    lasti=-1
    next=[0]*MaxSize 
    i,j=0,0
    GetNext(t,next)
    while i<s.getsize()and j<t.getsize():
        if j==-1 or s[i]==t[j]:
            i,j=i+1,j+1
        else:
            j=next[j]
        if j>=t.getsize():
            lasti=i-t.getsize()  #记录子串的位置
            j=0
        return lasti

设计一个算法，求一个n行n列的二维整型数组a的左下角-
右下角和右上角-左下角两条对角线的元素之和。
解：置s为0,用s累加a的左上角-右下角元素a[i]i之和，再用s累加a的右上角-左下角元素a[j]n-j-1之和。当n为奇数时，两条对角线有一个重叠的元素a[n/2][n/2]，需从s中减去。对应的算法如下：

1
2
3
4
5
6
7
8
9
10
def Diag(a): 
    s=0
    n=len(a)
    foriinrange(n)：
        s+=a[i][i]
    forjinrange(n)：
        s+=a[j][n-j-1]
    if n%2==1:
        s-=a[n//2][n//2]
    return s

设有一个不带表头结点的整数单链表p，设计一个递归算法getno(p,x)查找第一个值为x的结点的序号（假设首结点的序号为0），没有找到时返回-1。
解：设计getno1(p,x,no)算法，其中形参no表示p结点的序号，初始时p为首结点，no为0。
(1)p=None,返回-1。
(2)p.data=x,返回no。
(3)其他情况返回小问题getno1(p.next,x,no+1)的结果。
对应的递归算法如下：

1
2
3
4
5
6
7
8
9
def getno1(p,x,no):  
    if p==None:
        return -1
    if p.data==x:
        return no
    else: 
        return getno1(p.next,x,no+1)
    def getno(p,x):
        return getno1(p,x,0)

设有一个不带表头结点的整数单链表p，设计一个递归算法delx(p,x)删除单链表p中第一个值为x的结点。
解：设f(p,x)的功能是返回在单链表p中删除第一个值为x的结点后结果单链表的首结点。对应的递归模型如下：
f(p,x)=None 当p=None时
f(p,x)=p.next 当p.data==x时
f(p,x)=p(q=f(p.next,x),p.next=q)其他情况
对应的递归算法如下：

1
2
3
4
5
6
7
8
if p==None:
        return None
ifp.data==x:    #找到第一个值为x的结点
    return p.next
else: 
    q=delx(p.next,x)
    p.next=q         ＃连接起来
    return p

设有一个不带表头结点的整数单链表p，设计一个递归算法delxall(p,x)删除单链表p中所有值为x的结点。
解：设f(p,x)的功能是返回在单链表p中删除所有值为x的结点后结果单链表的首结点。对应的递归模型如下：

f(p,x)=None 当p=None时
f(p,x)=q(q=f(p.next,x)) 当p.data==x时
f(p,x)=p(q=f(p.next,x),p.next=q)其他情况对应的递归算法如下：

1
2
3
4
5
6
7
8
9
10
def delxall(p,x)：
    if p==None:
        return None
    if p.data==x:    ＃找到一个值为x的结点
        q=delxall(p.next,x) ＃在子单链表中删除
        return q         ＃返回删除后的结点
    else:  
        q=delxall(p.next,x)  ＃在子单链表中删除
        p.next=q       ＃连接起来
            return p

假设二叉树中每个结点值为单个字符，采用二叉链存储结构存储。试设计一个算法，求一颗给定二叉树bt中的所有大于x的结点个数。
解：可以采用任何遍历方法，这里采用用先序遍历。对应的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
def GreaterNodes(bt,x) :
    return_GreaterNodes(bt.b,x)
def _GreaterNodes(t,x):
    num=0
    if t==None:
        return 0
    else:
        if t.data>x: num+=1
        num1=_GreaterNodes(t.lchild,x)
        num2=_GreaterNodes(t.rchild,x)
        num+=numl+num2
        return num

假设二叉树中每个结点值为单个字符，采用二叉链存储结构存储。试设计一个算法，按从右到左的次序输出一颗二叉树bt中的所有叶子结点。
解：3种递归遍历算法都是先遍历左子树，再遍历右子树，这里只需要改为仅输出叶子结点，并且将左、右子树遍历的次序倒过来即可。以先序遍历为基础修改的算法如下：

1
2
3
4
5
6
7
8
def RePreOrder(bt)：＃求解算法
    _RePreOrder(bt.b)
def _RePreOrder(t)：
    if t!=None:
        if t.lchild==None and t.rchild==None:
            print(t.data,end=‘’)
        _RePreOrder(t.rchild)
        _RePreOrder(t.lchild)

给定一个带权有向图的邻接表存储结构G，创建对应的邻接矩阵存储结构g。
解：先将邻接矩阵g的元素初始化（g.edges[i][j]=0,其他置为
∞），然后遍历邻接表G的每个单链表，修改g中edges数组的相应元素。对应的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
def AdjToMat(G):
    g=MatGraph()
    g.n,g.e=G.n,G.e
    g.edges=[[0]*g.nfor iin range(g.n)]
    for iin range(g.n)：
        for j in range (g.n):
        if i!=j: g.edges[i][j]=INF
    else: g.edges[i] [j]=0
    for iin range (G.n):      ＃处理顶点i
        for j in range(len(G.adjlist[i])): ＃处理顶点i的所有出边
            w=G.adjlist[i][j].adjvex
            g.edges[i] [w]=G.adjlist[i][j]weight
    return g

一个长度为L（L大于等于1）的升序序列S，处在第éL/2ù个位置的
数称为S的中位数。例如，若序列S1=（11，13，15，17，19），则S1的中
位数是15。两个序列的中位数是含它们所有元素的升序序列的中位数。例如，
S2=（2，4，6，8，20），则S1和S2的中位数是11。现有两个等长升序序列A
和B,试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A
和B的中位数，并说明所设计算法的时间复杂度和空间复杂度。
解：两个升序序列分别采用int数组A和B存放。先求出两个升序序列A、B的 中位数，设为a和b。若a=b，则a或b即为所求的中位数；否则，舍弃a、b中
的较小者所在序列之较小一半，同时舍弃较大者所在序列之较大一半，要求
两次舍弃的元素个数相同。在保留的两个升序序列中重复上述过程，直到两
个序列中均只含一个元素时为止，则较小者即为所求的中位数。对应的算法 如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def FindMedian(A,B,n): ＃求解算法 
    startl,endl=0,n-1 
    start2,end2=0,n-1 
    while startl!=endl or start2!=end2: 
        midl=(startl+end1)//2 
        mid2=(start2+end2)//2
        if A[mid1]==B[mid2]:
            return A[midl]
        if A[mid1]<B[mid2]:
            if (startl+end1)%2==0: ＃若元素个数为奇数
                startl=midl ＃舍弃A中间点以前的部分且保留中间点
                end2=mid2 ＃舍弃B中间点以后的部分且保留中间点
            else: ＃若元素个数为偶数
                startl=midl+1 ＃舍弃A的前半部分
                end2=mid2 ＃舍弃B的后半部分
        else:
            if (startl+end1) %2==0: ＃若元素个数为奇数
                endl=midl ＃舍弃A中间点以后的部分且保留中间点
                start2=mid2 ＃舍弃B中间点以前的部分且保留中间点
            else: ＃若元素个数为偶数
                endl=midl ＃舍弃A的后半部分
                start2=mid2+1 ＃舍弃B的前半部分
    return A[startl] if A[startl]<B[start2] else B[start2]

上述算法的时间复杂度为O (log2n)，空间复杂度为O(1)
设计一个算法，输出在一颗二叉排序树中查找某个关键字k经过的查
找路径。
解：使用path列表存储经过的结点关键字，当找到关键字为k的结点时，向
path中添加k并返回；否则将当前结点t的关键字添加到path,再根据比较结
果在左或者右子树中递归查找。对应的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def SearchPath(bt,k) : ＃求解算法
    path=[]
    _SearchPath(bt.r,k,path)
    return path
def _SearchPath(t,k,path): ＃被SearchPath()调用
    if t==None: return
    elif k==t.key:
        path.append(k) ＃将k添加到路径中
        return
    else:
        path.append(t.key) ＃将当前结点的关键字添加到路径中
        if k<t.key:
            _SearchPath(t.lchild,k,path) ＃在左子树中递归查找
        else:
            _SearchPath(t.rchild,k,path) ＃在右子树中递归查找

编写一个实验程序，采用快速排序完成一个整数序列的递增 排序，要求输出每次划分的结果，并用相关数据进行测试。 解：快速排序的过程参见《教程》9.3.2节，每次以base为基准划分的 输出格式是“［左子序列］base[右子序列］”。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def disp(R,s,t,i)： ＃输出每一次划分的结果 
    print (“”，end=") 
    for j in range(s): 
        print ("",end=") 
    print ("[",end=”’) 
    for j in range (s,i): 
        print(“%3d”%(R[i])，end=‘’) 
    print("]%d["%(R[i]，end=‘’) 
    for j in range(i+1,t+1): 
        print("%3d"%(R[j]),end=‘’) 
    print("]") 
def Partition2(R,s,t): 
    i,j=s,t 
    base=R[s] ＃以表首元素为基准 
    while i!=j: ＃从表两端交替向中间遍历，直到 i=j为止 
        while j>i and R[j]>=base: 
            j-=1 ＃从后向前遍历，找一个小于基准的R[i] 
        if j>i:
            R[i]=R[j] ＃R[j]前移覆盖R[i] 
            i+=1
            while i<j and R[i]<=base: 
                i+=1 ＃从前向后遍历，找一个大于基准的R[i] 
            if i<j:
                R[j]=R[i] ＃R[i]后移覆盖R[j] 
                j-=1
        R[i]=base #基准归位
        return i ＃返回归位的位置
def MergeSort(R): #对R[0..n-1]按递增进行二路归并 
    length=1 
    while length<len(R): ＃进行log2n(取上界）趟归并 
        MergePass(R,length) 
        print("length=%d:"%(length),R) 
        length=2*length ＃主程序 
if _name_=='_main_’: 
    R=[6,8,7,9,0,1,3,2,4,5]
    print()
    print("初始序列”，end=‘’) 
    print(R)
    print(“排序过程”) MergeSort(R) print(“排序结果”，end=‘’）
    print (R)